| (1) |
| Main Contents | Help |
We start with the differential rate equation for a first order reaction. This
equation is a mathematical statement that the rate of change of the
concentration of A is proportional to the concentration of A at that
time.
| (1) |
this can be rearranged to:
| (2) |
which can now be integrated over time.
For the integration limits we will use the information
that initially ![]() at
at ![]() .
.
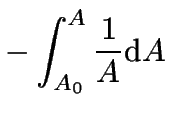 |
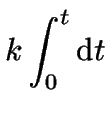 |
(3) | |
| (4) | |||
| (5) |
This is of the form y = slope x + intercept which is the equation for a straight line.
Therefore, for a first order reaction, if we plot the natural logarithm of [A] versus time we should obtain a straight line of slope = ``-k'' and intercept = ln[Ao]. With suitable data we can therefore calculate the specific rate constant k.
For second order kinetics the differential rate law is given by:
The integrated rate law for second order reactions where
![]() is:
is:
| (7) |
where x is the quantity of A or B that has reacted at time t.
In the special case that ![]() , the integration of
equation 6 is quite easy:
, the integration of
equation 6 is quite easy:
| (8) |
each side can be integrated like so:
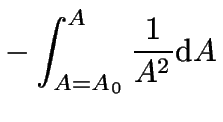 |
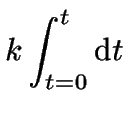 |
(9) | |
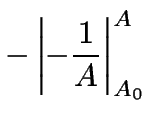 |
(10) | ||
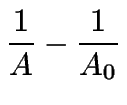 |
(11) | ||
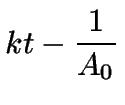 |
(12) |